
Von Simon Schöpf
Lesezeit: ca. 8 Minuten
Univ.-Prof. Dr. Tim Netzer ist Leiter des Instituts für Mathematik und forscht im Gebiet der reellen Algebra und Geometrie. Die meisten werden sich noch an Beispiele aus der Schulzeit erinnern: Geraden, Ebenen und Kurven können auch als Gleichungen dargestellt/definiert werden:
„Dieses Foto“ von Unbekannter Autor ist lizenziert gemäß CC BY-SA
Tim Netzer untersucht jedoch nicht Gleichungen, sondern Ungleichungen. Das heißt hier soll die Gleichung größer Null anstatt gleich Null sein. Dabei „entstehen“ ganz andere Objekte. Diese finden sich innerhalb und außerhalb der Mathematik z. B. in Bereichen der Optimierung oder auch der Quantenphysik.
Wir haben aber nicht nur über seine Forschung gesprochen, sondern auch über Mathematik im Allgemeinen, dazu später gleich mehr.
Methodische Vorgangsweise
Tim Netzer löst keine Gleichungen im engeren Sinn, sondern er versucht allgemeine Überlegungen anzustellen: Was lässt sich überhaupt durch welche Art von Gleichung beschreiben und was nicht?
„Wie kompliziert wird die Gleichung, wenn ich etwas Kompliziertes beschreiben möchte? Es sind also eher theoretische Überlegungen und nicht konkrete Beispiele, die gelöst werden“, erklärt uns der Forscher.
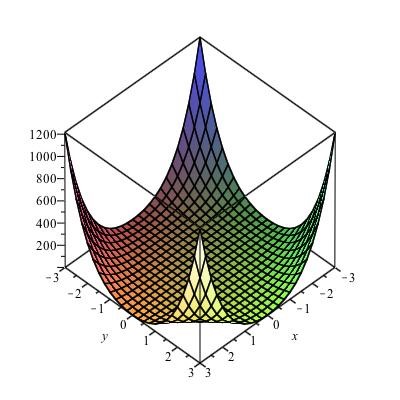
Auf einem Poster zeigt uns Netzer einen Graphen, der aussieht wie eine Gebirgslandschaft, welche durch eine Polynomfunktion beschrieben wird. Diese Polynomfunktion hat zwei Variablen, in welche reelle Zahlen eingesetzt werden. Dadurch entsteht ein „Gebirge“ über der Ebene.
Zu den reellen Zahlen gehören alle Zahlen, die auf der Zahlengerade liegen. Das mathematische Formelzeichen für diese Zahlenmenge lautet: ℝ. Die reellen Zahlen setzen sich aus den rationalen Zahlen (Bsp.: -3, -3/2, 0, 2/3, 5 usw.) und den irrationalen Zahlen (Bsp.: π, e, √3usw.) zusammen
Dieser Bereich der Forschung gehört zur geometrischen Grundlagenforschung und ist für Außenstehende sehr abstrakt:
„Wir arbeiten nicht mehr im dreidimensionalen Raum, sondern normalerweise im allgemeinen n-dimensionalen Raum und das ‚n‘ ist gar nicht spezifiziert, […] manchmal sogar in einem unendlich dimensionalen Raum. Die Vorstellung versagt dann natürlich völlig bei mir, genauso wie bei allen anderen auch. Es ist aber wichtig, sich eine Vorstellung zu machen von dem, was man tut, sonst kommt man nicht auf die richtigen Ideen. Da stelle ich mir, genauso wie jeder andere Mensch auch, den dreidimensionalen Raum vor, manchmal sogar nur den zweidimensionalen. Damit muss man sich dann behelfen und schauen, dass die Vorstellung, die man da entwickelt, gut genug ist, um auch Ideen zu bekommen, die man dann ganz formal in höher dimensionalen Räumen benutzen kann. Es ist also eine Illusion, dass Mathematiker sich sieben-dimensionale Räume vorstellen können, also ich zumindest kann das nicht,“ erläutert Netzer uns seine Vorgehensweise.
Forschungsalltag
Konkret sucht sich Tim Netzer ein interessantes Problem, indem er sich mit Arbeiten von anderen Wissenschaftler*innen befasst und sich mit diesen auch austauscht, „ein eher kommunikativer Prozess“ wie der Forscher festhält. Besonders wichtig sind hierbei Konferenzen und Tagungen, die Ideen liefern. Im Gegensatz zu einigen naturwissenschaftlichen Konferenzen, wo oftmals die Konkurrenz im Vordergrund steht, zeichnen sich die Mathematiker*innen durch Kooperationsbereitschaft auf:
„Ich bin froh, wenn sich andere Wissenschaftler*innen dafür interessieren, was ich mache; […] wenn wir dann gemeinsam darüber nachdenken und wenn wir was rauskriegen und wir gemeinsam eine Arbeit schreiben. Den Versuch, die anderen wegzuhalten und das alles allein zu machen, kenne ich überhaupt nicht. Das macht Konferenzen sehr angenehm, da ist kein ‚Hauen und Stechen‘. Das ist eher ein nettes Kaffeekränzchen unter der Familie, wo man sich gegenseitig hilft.“
Zurück im Büro nimmt Tim Netzer diese Idee und zeichnet oftmals dreidimensionale Bilder, um ein Gefühl zu bekommen, was „stimmen könnte und was nicht“. Die eigentliche Arbeit findet dann auf dem Papier bzw. der Tafel statt, um herauszufinden, ob der Beweis funktionieren kann, oder auch nicht. Dies kann ein langwieriger und frustrierender Teil der Arbeit sein, denn:
„In 99 Prozent der Fälle funktioniert der Beweis nicht und dann muss man die Tafel wieder löschen und sich wieder hinsetzen und wieder warten, bis die nächste Idee kommt.“
Kreative Lösungsansätze
„Ich überlege mir zum Beispiel, was für Arten von Mengen ich denn beschreiben kann, wenn ich mir Ungleichungen vom Grad drei erlaube. […] Obwohl per Definition ursprünglich einfach Gleichungen vom Grad drei erlaubt sind, muss ich, damit etwas Interessantes rauskommt, andere Beschreibungen finden: Wenn die Menge so aussieht, diese und jene Eigenschaft hat, dann kann ich sie durch eine Ungleichung vom Grad drei beschreiben. Diese Ideen, was andere Beschreibungen wären, die sinnvoll sind, die muss ich haben und wenn ich die Idee habe, muss ich überprüfen, ob sie stimmt“, erklärt uns der Forscher an einem Beispiel.
Diese Vorgehensweise unterscheidet sich sehr stark von der Mathematik in der Schule. Dort gibt es die Aufgabe und es gibt einen (oder mehrere) Wege, um zum Ergebnis zu kommen. Die größte Schwierigkeit ist es oft, sich nicht zu verrechnen. In der mathematischen Grundlagenforschung gibt es keine Vorgehensweise, die nachgeschlagen werden kann. Auch gibt es keine Standardmethode, nach welcher vorgegangen werden kann. Es ist ein kreativer Prozess, bei welchem es darum geht Probleme zu lösen, ohne zu wissen, wie diese gelöst werden sollen.
Wie Mathe zugänglicher werden könnte
Nicht nur Schüler*innen können Angst vor neuer, ihnen unbekannter Mathematik haben – Tim Netzer kennt dieses Gefühl, wenn er sich zum Teil die Arbeiten von anderen Mathematiker*innen ansieht. Seiner Meinung nach kann diese Angst bei Schüler*innen dazu führen, es von vornherein nicht zu probieren. Nach dem Motto: Ich verstehe es sowieso nicht, wieso sollte ich es dann überhaupt probieren! Aus diesem Grund versucht der Forscher in seinen Vorlesungen seinen Studierenden die Angst zu nehmen und ihnen Durchhaltevermögen gegen den Frust beizubringen.

Algebra vs. Blumenrätsel. Quelle: https://i.redd.it/iazrz4e1uzj31.png
Ein weiteres Problem ist, dass Mathe nicht zu verstehen sozial akzeptiert wird. Wer kennt denn nicht Eltern und/oder Bekannte, die von sich behaupten, dass sie Mathe in der Schule nicht verstanden haben. „Ich bin sicher, dass viel mehr Leute viel mehr Mathematik verstehen könnten als sie glauben,“ stellt Tim Netzer dazu klar. Dies sieht man auch an den Studierenden: Wer die ersten zwei bis drei Semester „durchhält“, schafft auch den Bachelor- oder Masterabschluss – es gibt kaum Studienabbrüche nach dieser ersten Zeit!
Tim Netzer sieht auch das Problem des „langweiligen“ Rechnens in der Schulmathematik: „Wenn die einzige Schwierigkeit ist, sich nicht zu verrechnen, dann ist das natürlich tödlich für die Motivation.“ Mathematik besteht eben nicht nur daraus, etwas auszurechnen, sondern Ideen zu entwickeln, um Probleme zu lösen. Knobel- und Rätselaufgaben sind sehr beliebt und sind viel „näher“ an der eigentlichen Mathematik als viele Aufgaben im Schulbereich.
Zwischendurch ein Rätsel: Du hast einen fünf Liter und einen drei Liter Kübel. Wie schaffst du es, ohne Hilfe von Messbecher/Waage/etc., exakt vier Liter abzumessen? Postet euren Lösungsweg gern in die Kommentare!
Aber auch das reine Aufzeigen von Anwendungsbereichen der Mathematik oder Bezügen zu anderen Wissenschaften reicht nicht unbedingt. Plakatives Beispiel: Ohne Mathematik würde es keine Smartphones geben – interessieren sich deswegen mehr Leute für Mathe, oder haben mehr Spaß daran, weil sie wissen, dass dort viel Mathematik genutzt wird?
„Die Freude, ganz allein ein Problem zu lösen, lernt man in der Schule kaum. Was ist denn das für eine Freude, die Funktion richtig abgeleitet zu haben? Die Null-Stelle ausgerechnet zu haben? Das ist ja ok, aber das ist überhaupt nicht zu vergleichen mit der Begeisterung, die ich empfinde, ein Problem mit einer eigenen Idee zu lösen. […] Es wäre schön, wenn die Mathematik in der Schule ein bisschen mehr in diese Richtung gehen würde“, hält Tim Netzer abschließend fest.
Institutshomepage
https://www.uibk.ac.at/mathematik/algebra/
Link zum Instagram-Profil
https://www.instagram.com/algebra_uibk/
Twitter
https://twitter.com/AlgebraUibk
YouTube Kanal von Tim Netzer
https://www.youtube.com/channel/UCeOqc4erLBNzmOtKWfLDe4w
